Inquiry Activity Summary
- So where do we get sin^2x + cos^2x =1? Well if we think back to our triangle, we can see in the picture below that x = cos, y= sin and r = 1, and if we square this, we and up with our identity above.
2. The two remaining identities can be derived from the identity above by dividing by cos^2x, so it would be sin^2x/cos^2x + 1 = 1/cos^2x we know from our reciprocal identity that 1/ cos^2x is equal to sec^2x and we know from our ratio identity that sin^2x/ cos^2x is equal to tan^2x so we are left with 1 + tan^2x = sec^2x To find the next one we dot he same steps except this time we divide by sin^2x which leaves us with 1 + cos^2x/ sin^2x = 1/ sin^2x after doing out identities, we are left with 1 + cot^2x = csc^2x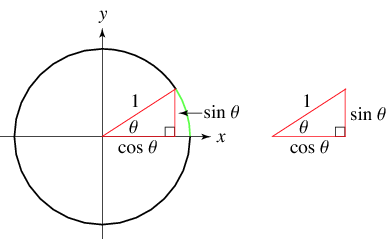
http://mathworld.wolfram.com/images/eps-gif/Trigonometry_1001.gif
Inquiry Activity Reflection
- The connections that I have noticed between these previous units, is that we have had to use previous knowledge from our unit circle, the ordered pairs ect. Another thing I've noticed is that we have taken our roots of our ratios, from previous ones such as the pythagorean theorem and we've had to alter the because these are no longer 90 degree triangles.
- If I had to describe trigonometry in three words, I would say that it's puzzling, challenging and intriguing.
No comments:
Post a Comment