1. Continuity is when a graph is predictable, has no breaks jumps or holes, can be drawn without lifting your pencil and has a value that is the same as the limit. Discontinuity is when a graph has any of these things or where the graph's value and limit aren't equal. There are different families of disc. they are removable and non-removable disc. In the removable family we have the point disc. which is similar to a hole, the limit still exists but the value does not unless these is another point on the same x value. In our next family non-removable we have jump which looks like what it sounds like a point jumping to a diff point and here the limit does not exist due to diff. left right. Also in this family we have oscillating which we tend to call wiggly because it is wiggly and the limit does not exist here because it is oscillating. The last type of disc in this family is infinite disc and the limit does not exist here because of unbounded behavior, in this kind of disc. we also have a vertical asymptote.
2. A limit is the intended height of a function, as so wonderfully explained above the only kind of disc in which a limit exists is at a point disc this is why the kinds of disc are divided into diff families. The limit is the intended height while the value is the actual height reached, this is why they can differ and exist while the other does not.
3. We evaluate limits numerically with a number table and place the limit in the center, from the left we subtract one tenth and keep getting it closer to the limit. And on the right we add one tenth and make it get closer to the limit. We evaluate a limit graphically by following the function from the left and the right and meet at the limit, if they don't meet then the limit does not exist. To solve a limit algebraically we use substitution where we plug it in and see what we get, if we get 0/0 then we move on to method two which is factoring where we try to factor something out and try to get things to cancel, and the last method is the rationalizing wherever the radical is and multiply by the conjugate.
Monday, May 19, 2014
Tuesday, April 22, 2014
BQ 3 Unit T Concepts 1-3
How do the graphs of sine and cosine relate to each of the others?
a. Tangent.
These graphs are different because we know that sin and cos are y/r and x/r so this is why neither of these graphs have asymptotes, r=1. Tangent on the other hand is y/x therefore wherever x or Cos is equal to zero, there is an asymptote.
b. Cotangent
Similar to tangent, cot is just x/y so wherever y or sin is equal to zero there is an asymptote, this is because the graph is undefined.
c. Secant
Because sec is r/x it will have asymptotes at the same places where tan had them but the two graphs look different because tan is only pi for a period and sec is relates to cos graph which is 2pi for a period.
d. Cosecant
Because csc is r/y it will have asymptotes at the same place where tan had them, and once again they are different because of the difference in the period length.
Thursday, April 17, 2014
BQ 5 Unit T Concepts 1-3
An asymptote is when the value of the graph is undefined, we know that something is undefined when it is divided by zero. Now let's take a look at our ratio identities tan is equal to y/x, cot equal to x/y, secant is r/x and cosecant is r/y, if we look at al of these we notice that these mean the numerator are divided by a number ;x, y these could be any number including 0. Meaning that any one of these could have an asymptote. If we look at cos and sin their ratio identities are y/r and x/r r will always equal one and therefore these will never be divided by 0, they won't have an asymptote.
Tan= y/x Sin= y/r
Cot= x/y Cos= x/r
Sec= r/x
Csc= r/y
Tan= y/x Sin= y/r
Cot= x/y Cos= x/r
Sec= r/x
Csc= r/y
Wednesday, April 16, 2014
BQ #2: Unit T Concept Intro
a) Why are the periods for sin and cos 2pi and the period for tan only pi?
If we look at all the signs that we have when looking at a sin graph, we can see that the order of this is; +,+,-,- this pattern does not repeat, therefore we need to have another cycle and then it will repeat, each of these cycles is equal to pi, therefore this graph's period will be 2pi
As for the cosine graph, the cycle is +,-,-,+ so we can see once again that the signs don't repeat themselves yet, therefore we had to once again add another cycle and make this period be 2pi.
When we look at the tan/cot graph however, we see that the cycle is +,-,+,- in this case the signs do repeat themselves so we have our pattern in only one cycle this makes a period of only pi.
b) If we think back to our ratio identities we know that sin is really y/r and cos is x/r we also know that r is always equal to 1 and then we can think about all our other ratios, tan y/x csc r/y ect r is no longer on the bottom, this means that the function isn't restricted to just one. Sin and cos are restricted because they will always be over r and r will always be equal to one, this is also why they have amplitudes of one.
If we look at all the signs that we have when looking at a sin graph, we can see that the order of this is; +,+,-,- this pattern does not repeat, therefore we need to have another cycle and then it will repeat, each of these cycles is equal to pi, therefore this graph's period will be 2pi
When we look at the tan/cot graph however, we see that the cycle is +,-,+,- in this case the signs do repeat themselves so we have our pattern in only one cycle this makes a period of only pi.
b) If we think back to our ratio identities we know that sin is really y/r and cos is x/r we also know that r is always equal to 1 and then we can think about all our other ratios, tan y/x csc r/y ect r is no longer on the bottom, this means that the function isn't restricted to just one. Sin and cos are restricted because they will always be over r and r will always be equal to one, this is also why they have amplitudes of one.
Thursday, April 3, 2014
Reflection #1 Unit Q: Verifying Trig Identities
1. To verify an identity means to try and get the left side of a problem equal to the right, to do this we usually have to simplify of use our ratios in order to make things cancel and reduce. Although the problem look like two different trig function when you begin, we are testing to verify that they can be reduced to equal the same thing.
2. Some tips that I have found helpful are to always think of things in terms of sin and cos, things may not seem similar until we convert them to these. I have also learned to keep in mind your pythagorean identities while working a problem out, so that we are sure not to change the ones we need, or so that we have a trig function we are trying to get to.
3. My first thought when looking at a trig problem is to see if I have any parts for my identities (are things squared, to i have one or two of the ratios needed?) next I check to see if the problem would be easier if I changed it into cos and sin. If these don't work I look to check if anything can be factored out or foiled ect. My final thought is to see if I square the problem would I have a solution or would the problem become easier when squared.
2. Some tips that I have found helpful are to always think of things in terms of sin and cos, things may not seem similar until we convert them to these. I have also learned to keep in mind your pythagorean identities while working a problem out, so that we are sure not to change the ones we need, or so that we have a trig function we are trying to get to.
3. My first thought when looking at a trig problem is to see if I have any parts for my identities (are things squared, to i have one or two of the ratios needed?) next I check to see if the problem would be easier if I changed it into cos and sin. If these don't work I look to check if anything can be factored out or foiled ect. My final thought is to see if I square the problem would I have a solution or would the problem become easier when squared.
Thursday, March 27, 2014
I/D #3 Unit Q Pythagorean Identities
Inquiry Activity Summary
- So where do we get sin^2x + cos^2x =1? Well if we think back to our triangle, we can see in the picture below that x = cos, y= sin and r = 1, and if we square this, we and up with our identity above.
2. The two remaining identities can be derived from the identity above by dividing by cos^2x, so it would be sin^2x/cos^2x + 1 = 1/cos^2x we know from our reciprocal identity that 1/ cos^2x is equal to sec^2x and we know from our ratio identity that sin^2x/ cos^2x is equal to tan^2x so we are left with 1 + tan^2x = sec^2x To find the next one we dot he same steps except this time we divide by sin^2x which leaves us with 1 + cos^2x/ sin^2x = 1/ sin^2x after doing out identities, we are left with 1 + cot^2x = csc^2x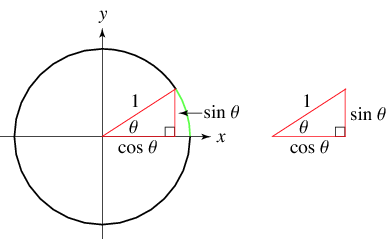
http://mathworld.wolfram.com/images/eps-gif/Trigonometry_1001.gif
Inquiry Activity Reflection
- The connections that I have noticed between these previous units, is that we have had to use previous knowledge from our unit circle, the ordered pairs ect. Another thing I've noticed is that we have taken our roots of our ratios, from previous ones such as the pythagorean theorem and we've had to alter the because these are no longer 90 degree triangles.
- If I had to describe trigonometry in three words, I would say that it's puzzling, challenging and intriguing.
Wednesday, March 26, 2014
SP #7 Unit Q Concept 2
This post was made in collaboration with Carlos Rendon, view other awesome math posts on his blog here
In our problem, we are given the information that sin<1 and also that cot is equal to -1/3
-Our first step was to find tan becasue we already have cot and we only have to do the reciprocal in order to get this. Our answer is -3 as shown in the picture below
-Now that we have tan, we can use the pythagorean identity 1 +tan ^2 = sec^2 so sec^2 is 1+ (9), radical 10
-We have sec so we can do the reciprocal in order to find cos, it is radical 10/ 10
-To find sin we can do 1- cos^2 and get 9/10, after we take the reciprocal and rationalize we should get 3 radical 10/ 10
-And to find csc we do the reciprocal of sin and get radical 10/ 3
In order to solve this using SohCahToa,
-We know sin is y/r which is 3/rad 10 and then it becomes 3rad 10/ 10 after we rationalize
-for csc it's r/y and it is rad10/ 3
- cos is x/r which is rad 10/10
-To get sec it's r/x and we get radical 10
-Next is tan, y/x which is -3
-And to get x/y (cot) it will be -1/3
In our problem, we are given the information that sin<1 and also that cot is equal to -1/3
-Our first step was to find tan becasue we already have cot and we only have to do the reciprocal in order to get this. Our answer is -3 as shown in the picture below
-Now that we have tan, we can use the pythagorean identity 1 +tan ^2 = sec^2 so sec^2 is 1+ (9), radical 10
-We have sec so we can do the reciprocal in order to find cos, it is radical 10/ 10
-To find sin we can do 1- cos^2 and get 9/10, after we take the reciprocal and rationalize we should get 3 radical 10/ 10
-And to find csc we do the reciprocal of sin and get radical 10/ 3
In order to solve this using SohCahToa,
-We know sin is y/r which is 3/rad 10 and then it becomes 3rad 10/ 10 after we rationalize
-for csc it's r/y and it is rad10/ 3
- cos is x/r which is rad 10/10
-To get sec it's r/x and we get radical 10
-Next is tan, y/x which is -3
-And to get x/y (cot) it will be -1/3
Friday, March 21, 2014
BQ #1 Unit P
Law of Sines- We need the law of sines whenever we only have two angles and a side of a triangle (ASA AAS). We use it by putting the sin of the angle divided by the side of that same letter, and then making it equal to the sin of an angle (if we have it) over the side of the same letter (we must have at least one of these in order for this to work)
Area Formulas- The Area of an oblique triangle formula is A= .5* side *side times sin of angle. We must be given two sides and one angle of the triangle. The original area formula is A= .5 b *h. In this formula we substitute the sides in and the sin.
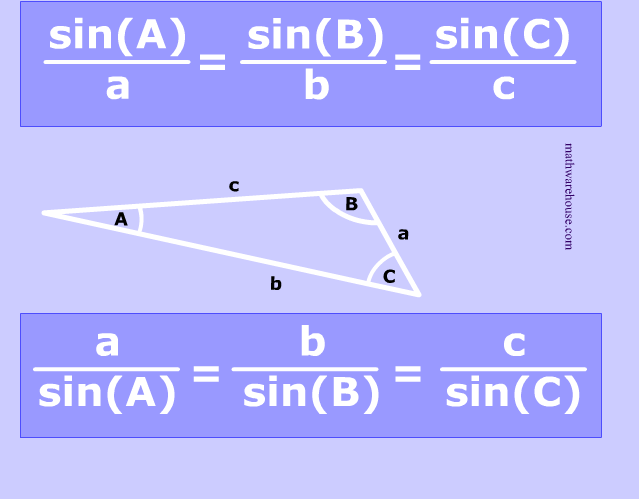 |
| http://www.mathwarehouse.com/trigonometry/law-of-sines/images/formula-picture-law-of-sines2.png |
Tuesday, March 18, 2014
WPP # 13 & 14: Unit P Concepts 6 & 7
Please see my WPP-13-14 made in collaboration with Carlos Rendon by visiting their blog here. Also be sure to check out their other awesome blog posts.
Thursday, March 6, 2014
WPP #12 Unit O Concept 10
 |
| http://piccolor.com/wp-content/uploads/2013/11/snow-mountain-wallpapers_22126_1920x1200.jpg |
Erica looks to the top of a snow mountain, the mountain is 270 ft. tall, the angle from where Erica is stranding to the top of the mountain is 34 degrees. How far away is erica from the mountain (round to the nearest foot).
- tan 34 = 270/x
- x = 270/(tan 34)
- x = 401 feet
Erica decides that she wants to ski down the mountain. When she reaches the top, she looks back down at the cabin she was staying in. The mountain height is still 270 and the cabin is 750 feet away, what is the angle?
-tan x = 270/ 750
- Inverse tan = 270/ 750
- angle = 19.8 degrees
Tuesday, March 4, 2014
I/D2: Unit O - How can we derive the patterns for our special right triangles?
Inquiry Activity Summary
For the 45-45-90 triangle, we take a square and cut it in half diagonally. We cut diagonally in order to make two of the sides 45 degrees (cutting 90 in half). We can get the hypotenuse by using the pythagor theorem and solving for c. We use the variable 'n' in order to show that this is a ratio, and can be expanded or condensed.
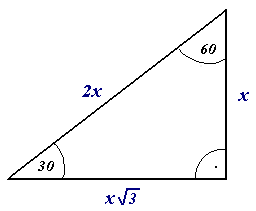
1) In order to get a 30-60-90 triangle from an equilateral triangle, we have to cut it down the middle.This makes the hypotenuse equal to 1 and the bottom side equal to 1/2, using the pythagorean theorem we get the last side which is radical 3 over 2. The final step is to multiply all our sides by 2 so that we get 2, 1, and radical 3. In order to show that this is a ratio and can be used with larger or smaller numbers, we use the variable n.
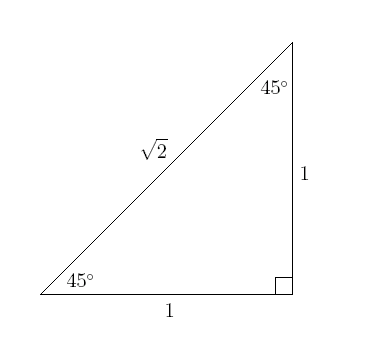
2) In order to derive a 45-45-90 triangle from a square, we have to cut it in half diagonally, making two of the angles 45 (because we cut 90 in half). This gives us a hypotenuse of radical 2 ( from the original square side) And the other two side are both 1. If we use the pythagorean theorem, we can check this and it is true.
3) It is important to note that we use variables in both of these to show that they can maintain the same ratio even if the numbers are altered, they all still have the same relationship.
1) In order to get a 30-60-90 triangle from an equilateral triangle, we have to cut it down the middle.This makes the hypotenuse equal to 1 and the bottom side equal to 1/2, using the pythagorean theorem we get the last side which is radical 3 over 2. The final step is to multiply all our sides by 2 so that we get 2, 1, and radical 3. In order to show that this is a ratio and can be used with larger or smaller numbers, we use the variable n.
 |
| http://www.freemathhelp.com/images/lessons/triangle306090-3.gif |
 |
| http://hotmath.com/hotmath_help/topics/45-45-90-triangles/triangle1.gif |
Inquiry Activity Reflection
1) Something I never noticed before about special right triangles is how they both come from other shapes, such as the square and the equilateral triangle, and we just have to cut them in half.
2) Being able to derive these patterns myself aids in my learning because if I ever forget the relationship that these triangles have, I can always go back and solve it from memory.
Saturday, February 22, 2014
I/D1: Unit N How do SRT and the UC relate?
 |
(http://upload.wikimedia.org/wikipedia/commons/1/15/Triangle_30-60-90_rotated.png)
|
1. The triangle above is a 30 degree triangle, the numbers around the edges are used as r (2x) x (y) and x rad 3(x). When we are using the ordered pairs we make r equal one and change the others so that the x remains the same.
 |
| (http://www.biology.arizona.edu/biomath/tutorials/trigonometric/graphics/trig_45_45_90.gif) |
2 The triangle to the left is a 45 degree triangle, and the major difference from the 30 degree triangle is that the x and y for this one are the same, we still want to have r be equal to 1.
| (https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcSUNhcyisjWpCaS61paVeoUvRYhYy01bc8iwclnXcNPlLpNSqoxfQ) |
3. This is the 60 degree triangle which is similar to the 30 degree triangle, we can see that the x and y are switched.
 |
| (http://literacy.purduecal.edu/STUDENT/mrrieste/quadrant1.png) |
 |
(http://1.bp.blogspot.com/-
Hr1ntVrUUK0/UF3p3LuRbLI/AAAAAAAAB5M/NMsjZCmV_vk/s1600/complete+unit+circle.jpg)
|
5. The same triangles go all the way around the unit circle, as we can see from the image to the left, the values obtain different signs when they are in different quadrants. In quadrant 1 they are all positive, in quadrant 2 the x's are negative and the y's are positive. In the 3rd quadrant they are both negative and in the 4th quadrant the y's are negative and the x's are positives.
Inquiry Activity Reflection
1. The coolest thing I learned from this activity is that the lines on a unit circle are really all just the same three triangles all the way around.2. This activity will help me in this unit because it made it easier for me to see that we add by 30 or 15 or 60 because these are the degrees of the three triangles.
3. Something I never realized about the special right triangles was that the ordered pairs on the unit circle are just the x and y after we make r equal to 1.
Works Cited
1. http://upload.wikimedia.org/wikipedia/commons/1/15/Triangle_30-60-90_rotated.png
2. http://www.biology.arizona.edu/biomath/tutorials/trigonometric/graphics/trig_45_45_90.gif
3. http://literacy.purduecal.edu/STUDENT/mrrieste/quadrant1.png
4. https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhH5ODpWbs47DCsR3WqGkJuxN_cT5GuWsgOW6jXXdLULLfVds02yP_m-PeVS6DOUus3XxYhrFd6MEgTPmPEE3YIpSrJKbrq0GqFIjenPq7gDV21eErAVpSWVSTY3O29AxQqIt9w3wRaha4T/s1600/complete+unit+circle.jpg
5. https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcSUNhcyisjWpCaS61paVeoUvRYhYy01bc8iwclnXcNPlLpNSqoxfQ
5. https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcSUNhcyisjWpCaS61paVeoUvRYhYy01bc8iwclnXcNPlLpNSqoxfQ
Monday, February 10, 2014
RWA #1 Unit: M Concepts: 4-6 Conic Sections
1. Parabola- the set of all points equidistant from a given point, known as the focus and a given line, known as the directrix.
2. -The formula for parabolas is: (x - h)^2 = 4p(y - k) or (y - k)^2 = 4p(x - h)
- In parabolas, the distance from the focus to the vertex, and the vertex to the directrix is known as 'p' this distance determines whether the parabola will be fat or skinny. In a parabola, the distance from the focus is the same for any given point. 'P' is also known as the focus.
"The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point on the axis of symmetry that intersects the parabola is called the "vertex", and it is the point where the curvature is greatest." (http://en.wikipedia.org/wiki/Parabola)
3. The picture above shows us where the vertex is located on the parabola, and the video also explains the other parts of the parabola and what their functions are.
- One of the most common uses of parabolas in the real world are roller coasters.They provide entertainment at amusement parks. Usually the roller coaster makes use of the outside of the parabola rather than the inside in order to be safer, the engineers have to be sure that the parabola is created well because is not, then it would not be safe.
As we can see int he picture below, there is a central support column which is where the vertex would be on a graph. There are only a couple supports because of the fact that because in parabolas the distance is the same from any point to the vertex, this means that if the engineers can create support columns in main parts of the roller coaster, then the parts that aren't supported by columns would be safe because the weight would be distributed equally.
2. -The formula for parabolas is: (x - h)^2 = 4p(y - k) or (y - k)^2 = 4p(x - h)

- In parabolas, the distance from the focus to the vertex, and the vertex to the directrix is known as 'p' this distance determines whether the parabola will be fat or skinny. In a parabola, the distance from the focus is the same for any given point. 'P' is also known as the focus.
"The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point on the axis of symmetry that intersects the parabola is called the "vertex", and it is the point where the curvature is greatest." (http://en.wikipedia.org/wiki/Parabola)
3. The picture above shows us where the vertex is located on the parabola, and the video also explains the other parts of the parabola and what their functions are.
- One of the most common uses of parabolas in the real world are roller coasters.They provide entertainment at amusement parks. Usually the roller coaster makes use of the outside of the parabola rather than the inside in order to be safer, the engineers have to be sure that the parabola is created well because is not, then it would not be safe.
As we can see int he picture below, there is a central support column which is where the vertex would be on a graph. There are only a couple supports because of the fact that because in parabolas the distance is the same from any point to the vertex, this means that if the engineers can create support columns in main parts of the roller coaster, then the parts that aren't supported by columns would be safe because the weight would be distributed equally.
4. Works Cited Page
- https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhvUoSGMbXCs7QfRZpJXFcLZexCyNN_4m3N6PR2ffMCfUey4Q6R1PwBsLfc9AQwMhI7IYQqYGbLh3cxiU75eDxIwZw1hpNrfVCxUc_YNgDfJfGF0sAVU5mH9bS6T-9fNVmDI9_eoL7CZXI/s1600/Screen+shot+2012-05-08+at+1.37.57+PM.png
- https://blogger.googleusercontent.com/img/proxy/AVvXsEi8RkhF1jy4qFSi00Iv5A3INwo1BwYS92aOT4o32L_eDFf1FjMSGJxcxjF5x9Xt18uci0vxnXKhnO5f93h6i8XytctCKRQ7ycr6KtUCIavZhlJuKTABOv6lMeYEv2-Fdi0jWjuRD25qfN9jyeBz1iXFZ6USitHwlGqCt2uHkNIIxv7Y_POTodU=
- http://mathforum.org/mathimages/index.php/Parabola
- http://youtube.com/parabolasdetailsections/
Subscribe to:
Comments (Atom)






